Reinforcement Learning from Human Feedback (RLHF) - Gridworld Agent
Published:
Reinforcement learning from human feedback
Lately, I’ve become really interested in a reinforcement learning from human feedback (RLHF). What caught my eye was how it’s used in ChatGPT and it seems like a lot of tech groups, like HuggingFace, are also keen on it. Even though some people aren’t sure if it’s the best approach, it’s viewed as a significant methodology for aligning ML systems with human values. With this project, I want to experiment the basics of RLHF using a really simple example.
Here are the basic steps of traing a simple grid traversing agent with RLHF:
- RL agent optimizes the current reward
- RL agent generates candidate trajectories
- Human feedback ranks trajectory based on preference
- Reward model is trained based on the HF-based trajectory ranking
- Current rewards are set to the trained reward
The reward model’s optimization is simply achived by cross-entropy loss based on the input of human preference labels. This approach ensures a simple and effective training process that converges the model’s predictitions towards human-aligned outputs.
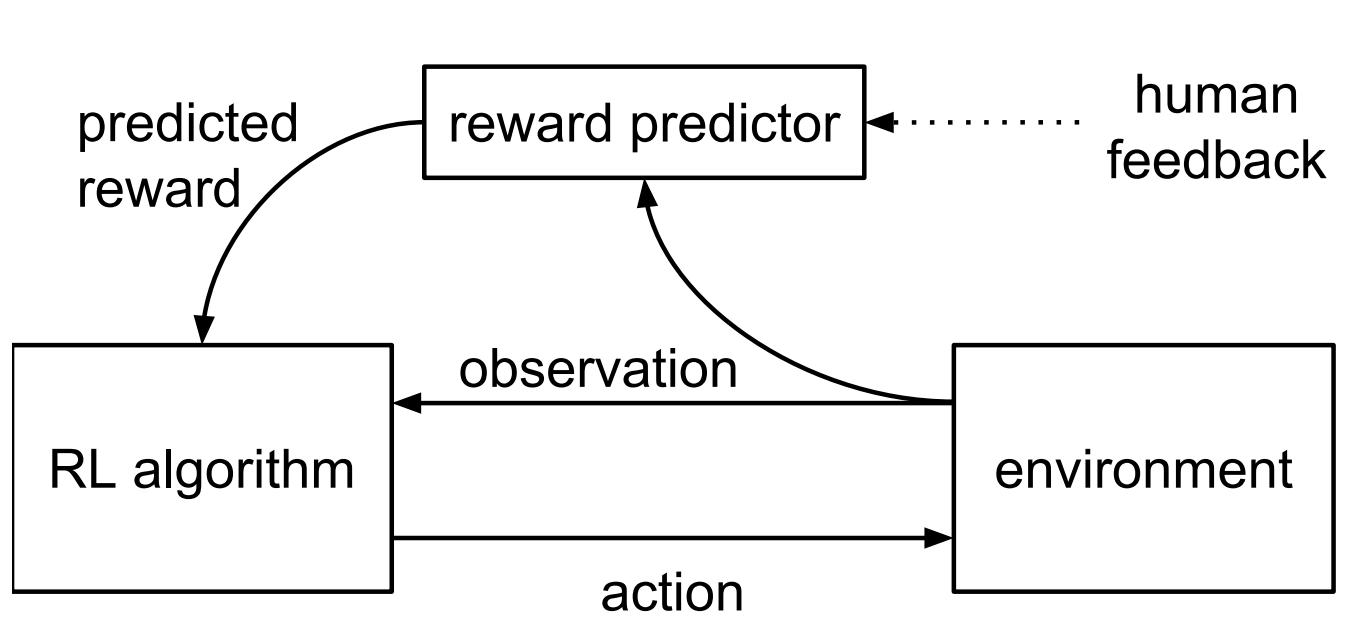
Basic Envionment Implementation
Here, I’ll use finite horizon soft value iteration in a closed form, with focus on reward learning. The environmetn is a deterministic $N \times N$ gridworld, which offers a clear visualization of reward learning’s impact on agent progression. For simulting a human evaluator, to avoid manually reanking the candidate trajectories, I use a sparse ground truth reward function, defined as $R_{\theta}(s, a) = \log P_{\theta}(s)$, with only the top-right state having a probability of 1. The agent is positioned intially at the bottom-left corner of the grid, ensuring a longer discovery phase for the target state in the initial iterations.
import itertools
import numpy as np
import torch
import torch.nn as nn
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sb
from tqdm import tqdm
import torch.nn.functional as Func
import torch.distributions as torchDistributions
Gridworld environment
class GridEnvironment:
def __init__(
self,
grid_count,
start_pos=np.array([]),
end_pos=np.array([]),
error=0.
):
assert error < 1.
self.grid_count = grid_count
self.state_dim = grid_count ** 2
self.act_dim = 5
self.action_labels = ["up", "right", "down", "left", "stay"]
self.error = error
state2position = list(itertools.product(np.arange(grid_count), np.arange(grid_count)))
self.state2position = np.array(state2position).reshape(self.state_dim, -1).astype(int)
if len(end_pos) == 0:
end_pos = np.array([[grid_count - 1, grid_count - 1]])
self.end_states = np.stack([self.position2state(p) for p in end_pos])
self.target_dist = np.zeros(self.state_dim)
self.target_dist[self.end_states] = 1./len(self.end_states)
self.reward_matrix = np.log(self.target_dist + 1e-6)
if len(start_pos) == 0:
start_states = np.ones(self.state_dim)
start_states[self.end_states] = 0.
self.start_states = np.where(start_states == 1)[0]
else:
self.start_states = np.stack([self.position2state(p) for p in start_pos])
self.start_dist = np.zeros(self.state_dim)
self.start_dist[self.start_states] = 1./len(self.start_states)
self.make_transition_matrix()
def position2state(self, position):
return np.where(np.all(position == self.state2position, axis=1))[0]
def value2map(self, v):
grid_count = self.grid_count
v_map = np.zeros((grid_count, grid_count))
for i in range(grid_count): # x pos
for j in range(grid_count): # y pos
v_map[j, i] = v[self.position2state(np.array([i, j]))]
return v_map
def make_transition_matrix(self):
transition = np.zeros((self.act_dim, self.state_dim, self.state_dim))
position = self.state2position.copy()
for a in range(self.act_dim):
next_position = position.copy()
next_error_position1 = position.copy()
next_error_position2 = position.copy()
if a == 0: # up
next_position[:, 1] = np.clip(next_position[:, 1] + 1, 0, self.grid_count - 1)
next_error_position1[:, 0] = np.clip(next_error_position1[:, 0] - 1, 0, self.grid_count - 1)
next_error_position2[:, 0] = np.clip(next_error_position2[:, 0] + 1, 0, self.grid_count - 1)
elif a == 1: # right
next_position[:, 0] = np.clip(next_position[:, 0] + 1, 0, self.grid_count - 1)
next_error_position1[:, 1] = np.clip(next_error_position1[:, 1] + 1, 0, self.grid_count - 1)
next_error_position2[:, 1] = np.clip(next_error_position2[:, 1] - 1, 0, self.grid_count - 1)
elif a == 2: # down
next_position[:, 1] = np.clip(next_position[:, 1] - 1, 0, self.grid_count - 1)
next_error_position1[:, 0] = np.clip(next_error_position1[:, 0] - 1, 0, self.grid_count - 1)
next_error_position2[:, 0] = np.clip(next_error_position2[:, 0] + 1, 0, self.grid_count - 1)
elif a == 3: # left
next_position[:, 0] = np.clip(next_position[:, 0] - 1, 0, self.grid_count - 1)
next_error_position1[:, 1] = np.clip(next_error_position1[:, 1] + 1, 0, self.grid_count - 1)
next_error_position2[:, 1] = np.clip(next_error_position2[:, 1] - 1, 0, self.grid_count - 1)
elif a == 4: # stay
pass
next_states = np.hstack([self.position2state(next_position[i]) for i in range(len(next_position))])
next_error_states1 = np.hstack(
[self.position2state(next_error_position1[i]) for i in range(len(next_error_position1))]
)
next_error_states2 = np.hstack(
[self.position2state(next_error_position2[i]) for i in range(len(next_error_position2))]
)
transition[a, np.arange(self.state_dim), next_states] += 1 - self.error
transition[a, np.arange(self.state_dim), next_error_states1] += self.error/2
transition[a, np.arange(self.state_dim), next_error_states2] += self.error/2
self.transition_matrix = transition
def reset(self, batch_size=1):
self.state = np.random.choice(np.arange(self.state_dim), size=(batch_size,), p=self.start_dist)
return self.state
def step(self, action):
state_dist = self.transition_matrix[action, self.state]
next_state = torch.multinomial(torch.from_numpy(state_dist), 1).numpy().flatten()
reward = self.reward_matrix[next_state]
self.state = next_state
ended = False
return next_state, reward, ended, {}
grid_count = 5
start_pos = np.array([[0, 0],])
end_pos = np.array([[4, 4],])
error = 0.
# test env
test_env = GridEnv(grid_count, start_pos=start_pos, end_pos=end_pos, error=error)
RLHF
def perform_value_iteration(transition_mat, reward_vec, plan_horizon, disc_factor=1., softmax_temp=1.):
""" Finite horizon discounted soft value iteration
Args:
transition_mat (torch.tensor): transition matrix. size=[act_dim, state_dim, state_dim]
reward_vec (torch.tensor): reward vector. size=[state_dim, act_dim]
plan_horizon (int): planning horizon.
disc_factor (float): discount factor.
softmax_temp (float): softmax temperature.
Returns:
q_func (torch.tensor): final Q function. size=[state_dim, act_dim]
"""
assert torch.all(torch.isclose(transition_mat.sum(-1), torch.ones(1)))
assert len(reward_vec.shape) == 2
state_dim = transition_mat.shape[-1]
act_dim = transition_mat.shape[0]
q_func = [torch.zeros(state_dim, act_dim)] + [torch.empty(0)] * (plan_horizon)
for i in range(plan_horizon):
v = torch.logsumexp(softmax_temp * q_func[i], dim=-1) / softmax_temp
ev = torch.einsum("kij, j -> ik", transition_mat, v)
q_func[i+1] = reward_vec + disc_factor * ev
return q_func[-1]
def execute_rollout(test_env, agent_obj, batch_size, max_steps):
data_dict = {"s": [], "a": [], "r": []}
s = test_env.reset(batch_size)
for t in range(max_steps):
a = agent_obj.select_action(s)
s_next, r, _, _ = test_env.step(a)
data_dict["s"].append(s)
data_dict["a"].append(a)
data_dict["r"].append(r)
s = s_next
data_dict["s"] = np.stack(data_dict["s"]).T
data_dict["a"] = np.stack(data_dict["a"]).T
data_dict["r"] = np.stack(data_dict["r"]).T
return data_dict
Here I define two class, Human and Agent;
The Human class is a synthetic human evaluator which provides rewards based on states. It has a evaluate method which takes two trajectories as inputs and returns a preference choice. The preference choice is 1 if the first trajectory is preferred, otherwise it’s 0.
The Agent class, which inherits from the PyTorch nn.Module class, defines an agent with reward parameters. This class has several methods:
target_dist: Returns the target distribution by applying a softmax function to the logarithm of the target state distribution.
reward: Returns the reward by applying a logarithmic softmax function to the target state distribution.
plan: Performs value iteration to compute the Q-function and the policy.
choose_action: Takes a batch of state indices as input and returns a batch of action indices.
evaluate: Similar to the evaluate function in the Human class, but this method is part of the Agent class and is used to evaluate the trajectories.
train_reward: Trains the reward model by minimizing the cross-entropy loss between the agent’s evaluations and the labels (human preferences).
The Agent class is initialized with a transition matrix, the planning horizon (T), learning rate, number of iterations for reward learning, and optionally the discount factor and softmax temperature. It also includes an optimizer to update the parameters of the reward model.
class Human:
""" Simulated user evaluator with state-based reward """
def __init__(self, reward_matrix):
self.reward_matrix = reward_matrix
def rank_trajectories(self, trajectory_1, trajectory_2):
"""
Args:
trajectory (dict): batch of trajectories with keys "state" and "action",
each of size=[batch_size, T]
Returns:
chosen_trajectory (np.array): user evaluation choices.
chosen_trajectory=1 if prefers trajectory_1 else chosen_trajectory=0. size=[batch_size]
"""
target_shape = trajectory_1["state"].shape
reward_1 = self.reward_matrix[trajectory_1["state"].flatten()].view(target_shape).sum(-1)
reward_2 = self.reward_matrix[trajectory_2["state"].flatten()].view(target_shape).sum(-1)
reward_combined = torch.stack([reward_1, reward_2], dim=1)
# select from preference probabilities
preference_probability = torch.softmax(reward_combined, dim=-1)
chosen_trajectory = torch.multinomial(preference_probability, 1).flatten()
# compute evaluation entropy
entropy = -torch.sum(preference_probability * torch.log(preference_probability + 1e-6), dim=-1).mean()
self.entropy = entropy.data.item()
return chosen_trajectory.numpy()
class Agent(nn.Module):
""" RLHF agent with reward parameters """
def __init__(self, transition_matrix, planning_horizon, learning_rate, iterations, discount_factor=1., temperature=1.):
super().__init__()
self.state_dim = transition_matrix.shape[-1]
self.action_dim = transition_matrix.shape[0]
self.transition_matrix = transition_matrix
self.planning_horizon = planning_horizon
self.discount_factor = discount_factor
self.temperature = temperature
self.learning_rate = learning_rate # reward learning rate
self.iterations = iterations # reward learning iterations
# parameterize reward as log target state distribution
self.log_target_distribution = nn.Parameter(torch.zeros(self.state_dim))
self.optimizer = torch.optim.Adam([self.log_target_distribution], lr=learning_rate)
def get_target_distribution(self):
return torch.softmax(self.log_target_distribution, dim=-1)
def calculate_reward(self):
return torch.log_softmax(self.log_target_distribution, dim=-1)
def create_plan(self):
with torch.no_grad():
q_values = value_iteration(
self.transition_matrix, self.calculate_reward().view(-1, 1), self.planning_horizon, self.discount_factor, self.temperature
)
self.q_values = q_values
self.policy = torch.softmax(self.temperature * q_values, dim=-1)
def select_action(self, state):
"""
Args:
state (np.array): batch of state indices. size=[batch_size]
Returns:
action (np.array): batch of actions indices. size=[batch_size]
"""
policy_for_state = self.policy[state]
action = torch.multinomial(policy_for_state, 1).flatten()
return action.numpy()
def rank_trajectories(self, trajectory_1, trajectory_2):
""" Mirrors Human rank_trajectories function """
target_shape = trajectory_1["state"].shape
reward = self.calculate_reward()
reward_1 = reward[trajectory_1["state"].flatten()].view(target_shape).sum(-1)
reward_2 = reward[trajectory_2["state"].flatten()].view(target_shape).sum(-1)
reward_combined = torch.stack([reward_1, reward_2], dim=1)
preference_probability = torch.softmax(reward_combined, dim=-1)
return preference_probability
def update_reward(self, trajectory_1, trajectory_2, labels):
for iteration in range(self.iterations):
preference_probability = self.rank_trajectories(trajectory_1, trajectory_2)
loss = -torch.log(preference_probability + 1e-6)[torch.arange(len(labels)), labels].mean()
loss.backward()
self.optimizer.step()
self.optimizer.zero_grad()
return loss.data.item()
torch.manual_seed(seed)
# Initialize agent and synthetic human
transition_matrix = torch.from_numpy(env.transition_matrix).to(torch.float32)
reward_matrix = torch.from_numpy(env.reward_matrix).to(torch.float32)
planning_horizon = 30
discount_factor = 1
softmax_temp = 1
learning_rate = 1e-2
iterations = 50
learning_agent = Agent(transition_matrix, planning_horizon, learning_rate, iterations, discount_factor, softmax_temp)
synthetic_human = Human(reward_matrix)
# Execute RLHF
batch_size = 100
max_trajectory_length = 30
total_iterations = 200
learning_history, sample_trajectory = run_rlhf(env, learning_agent, synthetic_human, batch_size, max_trajectory_length, total_iterations)
# Convert sampled paths to coordinates
number_of_paths = 10
maximum_path_length = 10
path_indices = np.arange(maximum_path_length, step=maximum_path_length // number_of_paths)
sampled_path_coordinates = []
for i in path_indices:
current_path = np.stack([env.state2pos[d] for d in sample_trajectory[i]["s"]]).astype(float)
current_path += np.random.normal(size=(len(current_path), max_trajectory_length, 2)) * 0.1
sampled_path_coordinates.append(current_path)
# Plot sampled paths on coordinates
fig, ax = plt.subplots(2, 5, figsize=(12, 6))
ax = ax.flat
for i in range(len(ax)):
ax[i].plot(sampled_path_coordinates[i][:, :, 0].T, sampled_path_coordinates[i][:, :, 1].T, "k-")
ax[i].plot(sampled_path_coordinates[i][:, 0, 0], sampled_path_coordinates[i][:, 0, 1], "go", label="start")
ax[i].plot(sampled_path_coordinates[i][:, -1, 0], sampled_path_coordinates[i][:, -1, 1], "ro", label="end")
ax[i].set_title(f"epoch {path_indices[i] + 1}")
ax[0].legend(loc="upper left")
plt.tight_layout()
plt.show()
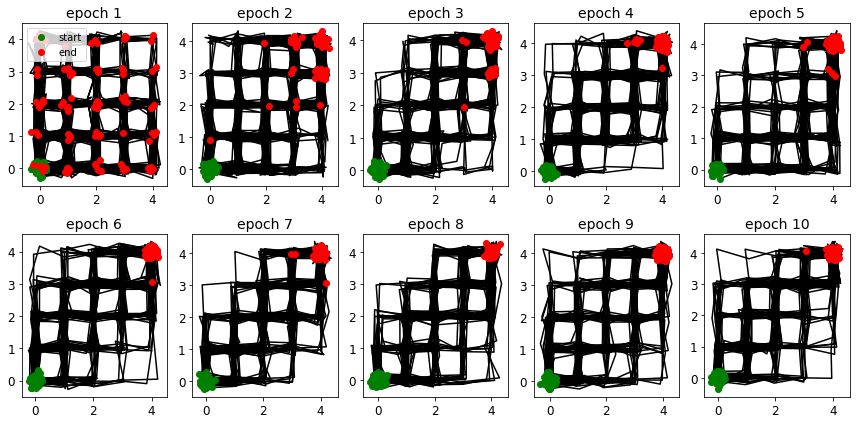
# Plot training history
fig, ax = plt.subplots(1, 3, figsize=(10, 4), sharex=True)
# Plot total reward over time
ax[0].plot(learning_history["reward"])
ax[0].set_xlabel("epoch")
ax[0].set_title("Cumulative Reward")
# Plot reward loss over time (binary cross entropy reward loss)
ax[1].plot(learning_history["loss"])
ax[1].set_xlabel("epoch")
ax[1].set_title("Reward Loss")
# Plot human preference distribution entropy over time
ax[2].plot(learning_history["entropy"])
ax[2].set_xlabel("epoch")
ax[2].set_title("Human Preference Entropy")
plt.tight_layout()
plt.show()
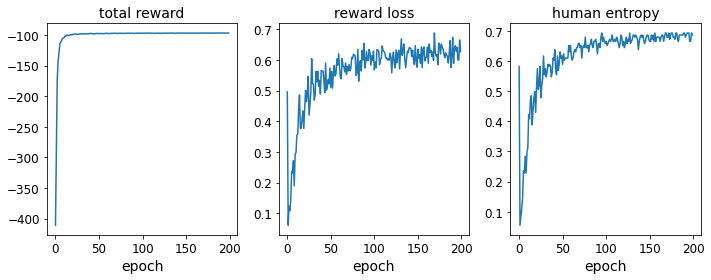
# No gradients are needed for this visualization
with torch.no_grad():
true_reward_map = env.value_to_map(env.target_distribution)
learned_reward_map = env.value_to_map(agent.distribution_target())
# Get the minimum and maximum values for the heatmap color scale
min_value, max_value = true_reward_map.min(), true_reward_map.max()
# Create a figure with two subplots
fig, ax = plt.subplots(1, 2, figsize=(8, 4))
# Create heatmaps of the true and learned rewards
sns.heatmap(true_reward_map, fmt=".2f", vmin=min_value, vmax=max_value, annot=True, cbar=False, cmap="Greys", ax=ax[0])
sns.heatmap(learned_reward_map, fmt=".2f", vmin=min_value, vmax=max_value, annot=True, cbar=False, cmap="Greys", ax=ax[1])
# Set the titles of the subplots
ax[0].set_title("True Reward Distribution")
ax[1].set_title("Learned Reward Distribution")
# Adjust the layout
plt.tight_layout()
plt.show()
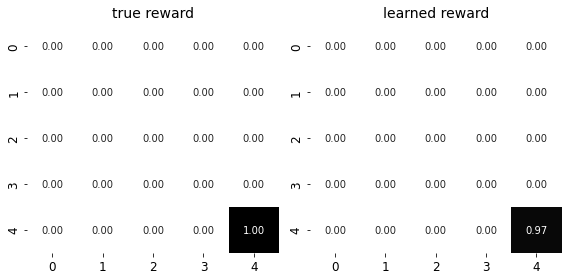
Results
From the cumulative reward curve, it’s clear that the RLHF agent is progressively improving at its task, navigating from the lower left to the upper right corner.
Observing the sample paths, there’s a clear shift from randomness in epoch 1 to a focused approach by epoch 10, with the majority reaching the target position. As a result, the task of judging trajectory quality becomes increasingly challenging for the human evaluator due to the high-quality paths produced by the agent. This manifests as rising reward loss and human entropy, indicating the random nature of the evaluator’s judgments.
Finally, the agent’s learned reward function aligns well with the true reward function, as evidenced by the heatmap comparison.
